性质

  1. 非空二叉树上的叶子节点数等于度为2的节点数+1，即n0n_{0} = n2n_{2} + 1。
  2. 非空二叉树上第 k 层上至多有 2k−12^{k-1}个节点（k≥1）。
  3. 高度为 h 的二叉树至多有 2h−12^{h}-1 个节点（h≥1）。
  4. 具有 n 个节点的完全二叉树的高度为（⌈log2(n+1)log_{2}(n+1)⌉或⌊log2nlog_{2}n⌋ + 1.

试题

**问题：**在一颗度数为 4 的树 T 中，若有 20 个度为 4 的节点，10 个度为 3 的节点，1 个度为 2 的节点，10 个度为 1 的节点，则树 T 的叶节点的个数是_____。

**分析：**设树中度为 i（i=0，1，2，3，4）的节点个数分别为 nin_{i}，树中节点总数为 n，则 n=分支数+1，而 分支数 = ∑各节点度数\sum_{}^{} \text{各节点度数}，即 n = 1+n1n_{1}+2n22n_{2}+3n33n_{3}+4n44n_{4} = n0n_{0}+n1n_{1}+n2n_{2}+n3n_{3}+n4n_{4}。
依题意得：1+n1n_{1}+2n22n_{2}+3n33n_{3}+4n44n_{4} = 123 = n0n_{0}+n1n_{1}+n2n_{2}+n3n_{3}+n4n_{4}，解得 n0n_{0} = 82.

问题： 已知一棵有2011个节点的树，其叶节点个数是116，该树对应的二叉树中无右孩子的节点个数是____。
分析： 这道题有些坑，看了好几遍题目，才终于明白它的意思。

问题： 设一棵非空完全二叉树T的所有叶节点均位于同一层，且每个非叶节点都有2个子节点。若T有k个叶节点，则T的节点总数是____。

首先我们看题目中说的是一棵有2011个节点的树，注意并没有明确指出是二叉树，在这种情况下这是一棵普通的树。然后题目中的说法是它对应的二叉树，这里就很奇怪了，树怎么对应二叉树呢？

其实这里隐藏的信息是树转二叉树算法，树转二叉树的逻辑倒不复杂，只有一个操作，对于树上的每一个节点，我们将它的第一个孩子节点当做它的左孩子，将它的右兄弟当做它的右孩子。如此一来，我们可以完成转化。

我从网上找来了一个例子，大家可以看下下图：

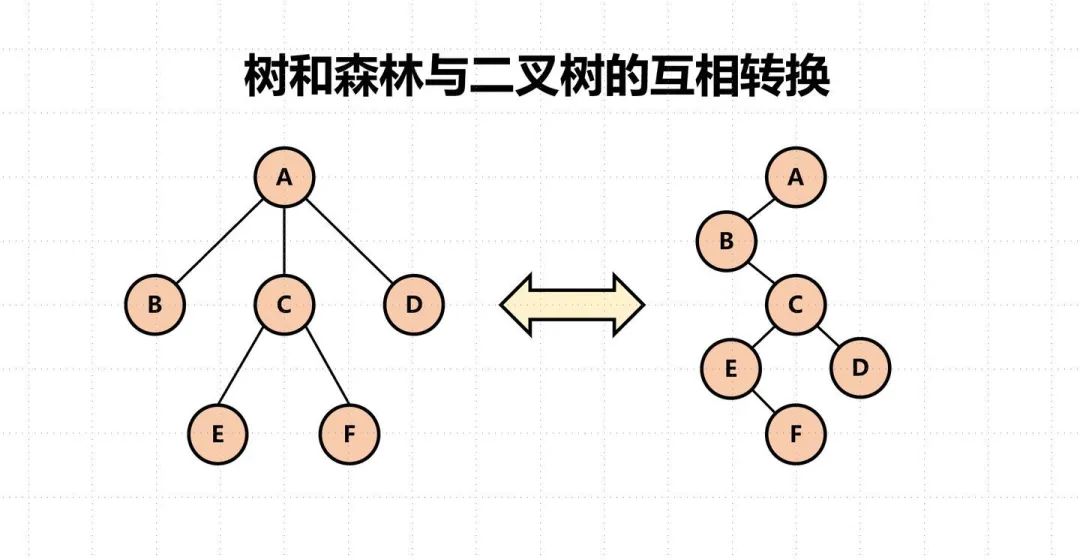
那这样转换之后我们怎么知道哪些节点没有右孩子节点呢？

我们还是需要从转换的算法上入手，由于我们在转换二叉树时是将右兄弟变成右孩子，所以没有右孩子的节点对应的就是转换之前没有右兄弟的节点。问题就变成了要求原树当中有多少个节点没有右兄弟。

到这里很多人就蒙圈了，这怎么求？

其实有办法求，并且还很简单。已知我们一共有2011个树节点，其中116个是叶子节点。众所周知叶子节点即没有孩子节点的节点，也就是说有2011-116个节点拥有孩子节点。很明显，对于每个拥有孩子节点的节点来说，它一定有且只有一个孩子节点没有右兄弟，即最右边那个。那么很显然，一共有2011-116=1895个节点没有右兄弟。

别忘了根节点也没有右兄弟，所以要加上根节点的1，答案就是1896。

指针

非空指针数 = 总分支数 = n - 1
空指针数 = 2 × 节点总数 - 非空指针数 = 2n - （n-1) = n+1

二叉树与深林的转化

树转二叉树：

  1. 规则：每个节点左指针指向他的第一个孩子，右指针指向他在树中相邻右兄弟，这个规则又称为“左孩子右兄弟”。由于根节点没有兄弟，所以对应的二叉树没有右子树。
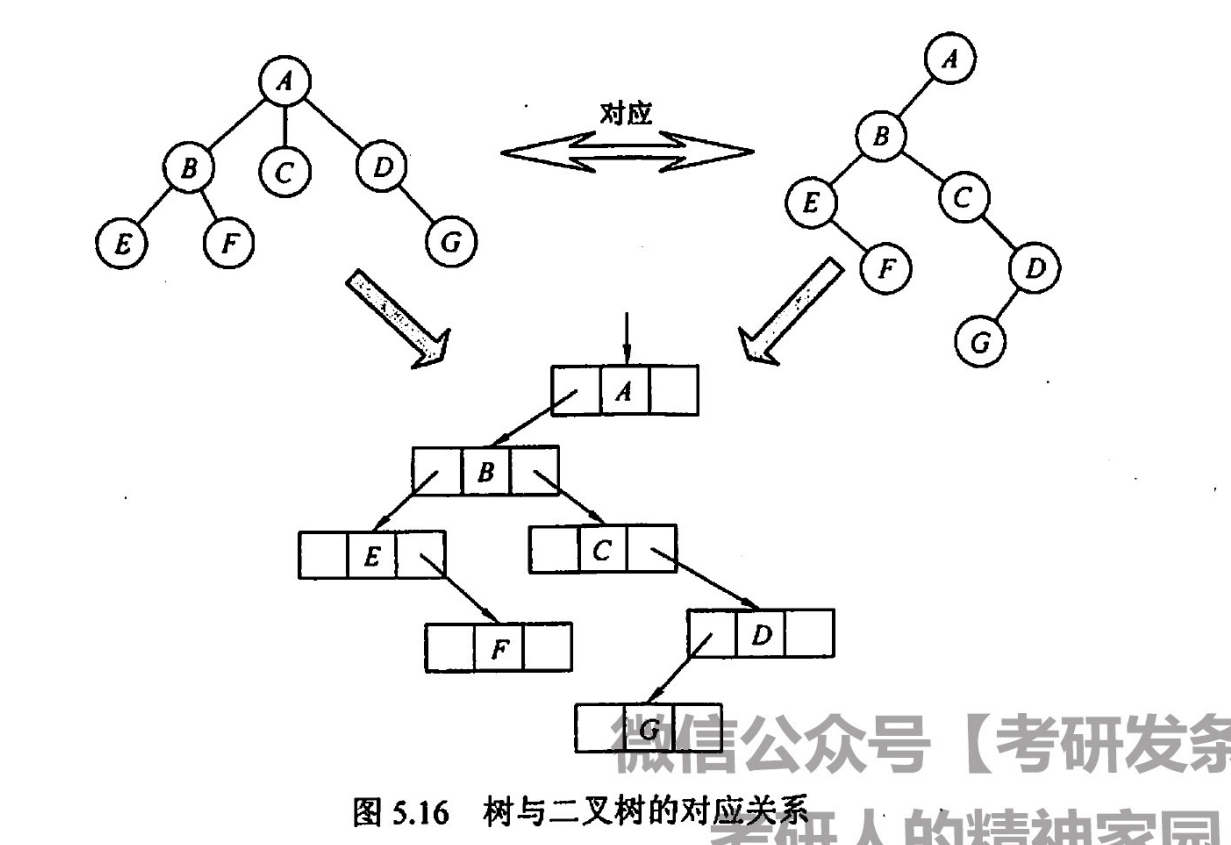
  2. 画法：在兄弟节点之间加一条线；对每个节点，只保留它与第一个孩子的连线，而与其他孩子的连线都抹掉；

森林转二叉树

  1. 规则：与树转二叉树类似，先将森林中的每颗树转换为二叉树，由于任何一颗和树对应的二叉树右子树必空，若把森林中第二棵树根视为第一棵树根的右兄弟，即将第二棵树对应的二叉树当作第一棵树根的右子树......，以此类推，就可以将森林转换为二叉树。
  2. 画法：将森林中的每棵树转换成对应的二叉树；每棵树的根也可视为兄弟关系，在每棵树的根之间加一个线。

二叉树转森林

  1. 规则：若二叉树非空，则二叉树的根及其左子树为第一棵树的二叉树形式，故将根的右链断开。二叉树根的右子树棵视为一个由除第一棵树外的森林转换后的二叉树，应用同样的方法，知道最后只剩一颗没有右子树的二叉树位置，最后再将每颗二叉树依次转换成树，就得到了原森林。